1. cache容量大小对效率的影响
对于给定容量大小的cache,cache容量=块数量×块大小,块越大,总的块数量越少。
容量更大的块可以通过挖掘空间局部性来降低失效率。随着块大小的增长, 失效率通常都在下降,这是比较好理解的。但如果单个块大小占 cache 容量的比例增加到一定程度,失效率最终会随之上升,这是因为:
- cache 中可存放的块数变少了。某个数据块会在它的大量数据被访问之前就被挤出 cache。
- 对于一个较大的数据块,块中各字之间的空间局部性也会随之降低,失效率降低带来的好处也就随之减少。
增大cache块大小时,另一个更严重的问题是大数据块带来的失效损失中的长延迟问题。失效损失是从下一级存储获得数据块并加载到 cache 的时间。该时间分为两部分:访问命中的时间和数据的传输时间。传输时间(也可以说是失效损失)将随着数据块的增大而增大。 而且,随着数据块的增大,失效率改善带来的收益开始降低。最终的结果是,失效损失增大引起的性能下降超过了失效率降低带来的收益,cache 性能当然随之下降。
失效率与块容量的关系图如下图所示(图示与相联度无关):
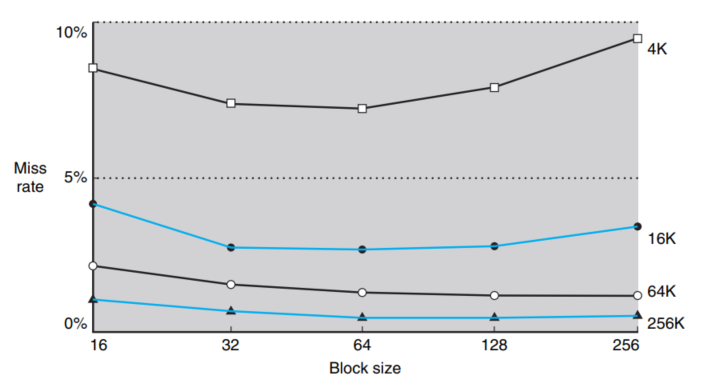
从不同的折线可以看到,对于不容容量大小的cache,失效率是随着cache块的增大先降低后上升的,cache块大小为64bit的时候失效率大致是最低。从不同折线间可以看出,同一cache块大小,cache容量越大,失效率越低,但失效率的降低率明显是递减的。
其实,对于大数据块带来的失效损失中的长延迟问题,也有一些解决办法,这里仅做简要叙述:
- 提早重启 (early restart)技术:即只要数据块中的所需数据返回来,就继续执行,无须等到该数据块中所 有数据都完成传输。这个技术对于icache(instruction cache)效果显著,指令访问很大程度上是顺序的,如果存储器系统可以每个时钟周期传送一个字,则处理器可能能够在返回所请求的字时重新启动操作。但对于dcache(data cache)效果不好,因为所需数据的访问顺序很难预测,在数据传输完成之前,下一个所需数据来自另一个数据块的概率比较大。如果由于当前数据传输未完成导致处理器不能继续访问数据 cache, 那么流水线就必 停顿。
- 重新组织存储(organize the memory)技术:首先将被请求的字(word)从内存传输到cache中。然后,从请求的字后面的地址开始,传输剩余的块,并回绕到块的开始。这种技术,被称为 "请求字优先(requested word first)" 或 "关键字优先(critical word first)" ,可能比早期重启稍微快一些,但它受到限制的属性与早期重启相同。(说大白话就是优先传输想要的数据,这个数据可能来源于主存块的中间某个部分,接着从想要数据的地址开始,传输剩余部分,包括前后的数据。这里的地址变化就像AHB协议中的wrap burst传输。那么传回cache的数据块中顺序可能是被打乱了的,所以叫重新组织存储技术)
2. cache 的性能评估和改进
2.1 cache性能评估
2.1.1 性能评估
CPU 时间可被分成 CPU 用于执行程序的时间和 CPU 用来等待访存的时间。通常,假设cache 命中的访问时间只是正常 CPU 执行时间的一部分。因此,
CPU时间 =(CPU执行的时钟周期数 + 等待存储访问的时钟周期数)X 时钟周期。
等待存储访问的时钟周期数可以被定义为,读操作带来的停顿周期数加上写操作带来的停顿周期数:
等待存储访问的时钟周期数 = 读操作带来的停顿周期数 + 写操作带来的停顿周期数。
读操作带来的停顿周期数可以由每个程序的读操作次数、读操作失效率和读操作的失效代价来定义:
读操作带来的停顿周期数 =读操作数目/程序 x 读失效率 x 读失效代价。
写操作要更复杂些。对于写穿透策略,有两个停顿的来源:一个是写失效,通常在连续写之前需要将数据块取回;另一个是写缓冲停顿,通常在写缓冲满时进行写操作会引发该停顿。因此,写操作带来的停顿周期数等于下面两部分的总和:
写操作带来的停顿周期数 = 写操作数目/程序 X 写失效率 X 写失效代价 + 写缓冲满时的停顿周期
由于写缓冲停顿主要依赖于写操作的密集度,而不只是它的频度,不可能给出一个简单的计算此类停顿的等式。如果系统中有一个容量合理的写缓冲(例如,四个或者更多字), 同时主存接收写请求的速度能够大于程序的平均写速度,写缓冲引起的停顿将会很少,几乎能够忽略。如果系统不能满足这些要求,那么这个设计可能不合理。设计者要么使用更深的写缓冲,要么使用写返回策略。写返回策略也会额外增加停顿,主要来源于当数据块被替换并需要将其写回到主存时。
在大多数写穿透 cache 的结构中,读和写的失效代价是相同的(都是将数据块从内存取至cache所花的时间)。假设写缓冲停顿是可以忽略不计的,就可以使用失效率和失效代价来 同时刻画读操作和写操作:
等待存储访问的时钟周期数 = 访存操作数目/程序 X 写失效率 X 写失效代价
也可以写为:
等待存储访问的时钟周期数 = 指令数目/程序 X 失效次数/指令数目 X 写失效代价
2.1.2计算cache性能举例
假设指令 cache 的失效率为 2%, 数据 cache 的失效率为 4%。如果处理器的 CPI 为 2, 没有任何的访存停顿;对于所有的失效,失效代价都为 100 个时钟周期。如果配置了一个从不失效的完美 cache, 那么处理器的性能会提高多少?假设 load 和 store 指令占所有指令 的 36%。
假设指令数目为I, 则指令访存失效的周期数为:指令访存失效周期数 =I x 2% x 100 = 2.00 x I。由于 load 和 store 指令占总指令数的 36%, 则数据访存失效的周期数为:数据访存失效周期数 =I × 36% × 4% × 100= 1.44 x I。存储访问失效的周期数为 2.00 I + 1.44 I = 3.44 I 这意味着平均每条指令等待存储访问的周期数大于 3。相应的,考虑了存储访问停顿的 CPI 为 2 + 3.44 = 5.44。由于指令数目或者时 钟频率都不变,则 CPU 执行时间的比率为:
$frac{带有存储访问停顿的CPU执行时间}{具有完美cache的CPU执行时间}=frac{I×CPI{stall}×时钟周期}{I×CPI{perfect}×时钟周期}=frac{CPI{stall}}{CPI{perfect}}=frac{5.44}{2}$
具有完美 cache 的 CPU 性能是原来的 5.44/2= 2.72 倍。
如果处理器运行得更快,用于存储访问停 顿的时间占整个执行时间的比例在不断增大。假设在前面的例子中,使用一个改进的流水 线,将 CPI 从 2 变为 1, 时钟频率不变,则处理器的性能在提升。那么考虑了 cache 失效的系统将会让CPI变为1 + 3.44 = 4.44。与配置完美 cache 的系统相比,两者的比率为:$frac{4.44}{1}=4.44$。
那么用于存储访问的停顿周期占总周期数的比例将会从$frac{3.44}{5.44}=0.63$变为$frac{3.44}{4.44}=0.77$
同理,如果不改变存储体系结构,仅提高时钟频率,由于 cache 失效带来的系统性能损失所占比例也会增大。
之前的例子和等式都假设命中时间不是影响 cache 性能的重要因素,如果命中时间增加,在存储系统中访问一个字所花的时间也在增加。这可能引起处理器时钟周期的增大。导致cache命中的时间增加一个最直观的原因就是cache容量的增加,更大的 cache 自然会有更长的访问时间(命中时间的增加可能会为流水线增加一个流水级,这样即使cache命中也会花费多个时钟周期。计算加深流水线对性能的影响则更为复杂)。对于提升大容量cache的性能来说,命中时间的减少比命中率的提升更占优势,命中时间的增加更容易将会导致处理器性能的下降。
为了说明不论命中还是失效访问数据存储的时间都会影响性能,设计者采用平均存储访问时间(Average Memory Access Time, AMAT) 作为指标来衡量不同的 cache 设计。平均存储访问时间是考虑了命中、失效以及不同访问频度的影响后的平均访存时间,定义如下:AMAT= 命中时间+ 失效率 x 失效代价
2.2 cache性能改进
改进cache性能最直接简单的方法主要有两种,分别是映射方式与cache块替换策略和多级cache。
-
映射方式与cache块替换策略
从各映射方式的关联度角度来说:关联度越低,命中率越低,因此直接映射命中率最低,全相联映射命中率最高。关联度越低,判断是否命中的开销越小,命中时间越短,因此直接映射的命中时间最短,全相联映射命中时间最长。所以,各映射方式在提高cache性能时,存在命中率和命中时间的折中问题,需要选择一个合适的关联度,平衡命中率与命中时间。
在块替换策略上,也有很多种,比如之前提到的随机算法RAND、先进先出算法FIFO、近期最少使用算法LRU、最不经常使用算法,此外,还有一些其他更复杂的替换算法,这里发个链接:经典论文解读——Cache 替换算法 - 多级缓存(multilevel caching)
所有的现代计算机都使用 cache。为了减小现代处理器高速时钟频率与访问 DRAM 所需 的不断增长的延迟之间的差距,大多数微处理器支持不同层级的缓存。二级 cache 一般与一 级 cache 封装在同一颗芯片中,一级 cache 失效后就会访问下一级缓存。如果二级 cache 中 有所需数据,一级 cache 的失效代价就是二级 cache 的访问时间,这和主存的访问时间相比 要少得多。如果一级或二级 cache 中都没有包含所需数据,就需要访问主存,那么失效代价 则会增大。
使用二级 cache 对处理器性能提升有多大的影响?下面的例子给出说明:
假设如果所有的存储访问在一级 cache 命中,则基准处理器的 CPI 为 1.0, 时钟频率为 4GHz。假设主存的访问时间为 100ns, 包括所有的失效处理过程。一级 cache 中每条指令的 平均失效率为 2%。 如果增加一个二级 cache, 不论失效或命中其访问时间都为 5ns, 其容量足够大,可以将失效率降低到 0.5%。问(增加了二级 cache 的)处理器增速多少?- 主存失效代价
主存的失效代价:$frac{100ns}{0.25ns}=100$个时钟周期 - 一级cache的CPI
带有一级 cache 的处理器 CPI 公式如下:
实际 CPI = 基准 CPI + 平均每条指令产 生的存储访问周期数=1.0 + 平均每条指令产生的存储访问周期数 = 1.0 + 2%x400 = 9 - 二级cache的CPI
对于带有二级 cache 的处理器,一级 cache 的失效可以通过访问二级 cache 或主存来处理。 二级 cache 的失效代价为:$frac{5ns}{0.25ns}=20$个时钟周期。如果在二级cache中失效,那就需要访问主存,则完整的失效代价为二级cache的访问时间与主存访问时间之和。因此,对于带有二级cache的处理器来说,实际CPI等于基准CPI与各级cache的访问时间之和。
实际CPI = 1 + 平均每条指令的一级cache 访问周期数 + 平均每条指令的二级cache访问周期数 = 1 + 2% x 20 + 0.5% x 400 = I + 0.4 + 2.0 = 3.4
因此,增加了二级 cache 的处理器增速:$frac{9.0}{3.4}=2.6$
- 主存失效代价
对于一级和二级 cache, 设计考虑是明显不同的。这是因为相比于单独一个cache来说, 其他 cache 层次的存在会改变其最佳策略的选择。特别地,两级 cache 结构允许其一级cache关注命中时间最小化以提高工作频率或关注流水级数的减少,同时其二级cache关注失效率来降低长访存延迟带来的失效代价。
与单个cache相比, 多级 cache (multilevel cache) 中的一级cache通常都较小。而且,一级cache会使用较小的数据 块容量,以配合较小的cache容量,降低失效代价。相对的,二级cache会比单个cache容量大很多,因为二级cache的访问时间没有那么关键。随着容量的增大,相比于单个cache, 二级cache会使用更大的数据块。由于更关注降低失效率,二级cache也会使用比一级cache更高的相联度。
总结:对于两级cache,第一级cache容量较小,更关注减小命中时间,以提高工作频率或者减小流水线级数;第二级cache容量较大,更关注提高命中率,以降低长访存延迟带来的失效代价。
多级cache作为一种降低失效代价的技术,它允许一级cache的失效访问去访问容量更大的二级 cache。通常,二级cache的容量会是一级cache的10倍或更大,可以处理很多一级cache中失效的访问。这时,失效代价就变为二级cache的访问时间(通常小于10个处理器时钟周期)与主存的访问时间(通常大于100个处理器时钟周期)的折中。



